Volume 3, numéro 1 – 2024 : VARIA
Compétence langagière et résolution de problèmes mathématiques chez les élèves des Cours moyens 2 des écoles primaires de l’arrondissement de Goulfey
Alhadji MAHAMAT
Introduction
La capacité à raisonner logiquement et à présenter les arguments convaincants est une compétence utile dans les systèmes éducatifs autant dans les pays industrialisés que dans les pays en développement. La compétence langagière nécessaire à résoudre les problèmes mathématiques est souvent citée comme l’une des compétences clés du XXIe siècle. À partir de la résolution de problèmes mathématiques, les élèves n’apprennent mieux que s’ils et elles savent bien lire le problème, le comprendre, le traduire en ses propres mots afin d’aboutir à un raisonnement logique. Cependant, dans les zones d’éducation prioritaire du Cameroun, la grande majorité des élèves des écoles primaires ont des difficultés à mobiliser cette compétence langagière et à l’utiliser dans les situations spécifiques afin de résoudre les problèmes mathématiques.
Le Cameroun est un pays qui se caractérise par une diversité linguistique et culturelle. Cette situation hétérogène a également un impact sur les connaissances et les pratiques linguistiques des apprenant·es qui peuvent éprouver des difficultés relativement au maniement de la langue d’enseignement. Dans son rapport sur l’évaluation des performances des systèmes éducatifs des pays de l’Afrique subsaharienne, le Programme d’analyse des systèmes éducatifs de la Confédération des ministres de l’Éducation des États et Gouvernement de la francophonie (PASEC) relève que
Dans la majorité des pays, la langue d’enseignement n’est souvent pas la langue maternelle des élèves, et ils la pratiquent peu dans leur vie quotidienne. C’est le cas du Bénin, du Burkina Faso, du Cameroun francophone, du Congo, de la Côte d’Ivoire, du Niger, du Sénégal, du Tchad et du Togo, pour le français, et du Cameroun anglophone, pour l’anglais (PASEC, 2016, p. 20).
En outre, dans les établissements d’enseignement secondaire, la situation linguistique se complexifie encore dans la mesure où s’ajoutent les langues vivantes 2 au secondaire tels que l’espagnol, l’allemand, l’arabe, l’italien, le chinois, etc. qui sont des langues souvent négligées par les élèves.
Depuis quelques années, des recherches basées sur les approches socioculturelles encouragent la mise en avant des pratiques de classe à travers la communication et l’utilisation de la langue inhérente aux apprentissages. Martin et Houssemand (cités par Vlassis, 2018, p. 2) ont mentionné que « le bilinguisme qui est sous-tendu par les langues vernaculaires réduit fortement à la fois l’efficacité et l’équité du système éducatif ». En s’intéressant à l’apprentissage des mathématiques dans les classes multilingues luxembourgeoises, Vlassis observe que
La maîtrise (formelle) surtout de l’allemand, mais aussi du français, constitue un facteur de sélection très fort alors que certaines compétences langagières des enfants sont négligées. Ainsi, la non-maîtrise formelle de la langue empêche en partie l’accès à des apprentissages comme les mathématiques, soit par le biais d’une interdiction d’accès à certaines filières scolaires, soit par le biais d’une maîtrise insuffisante de la langue véhiculaire de ces branches (Vlassis, 2018, section 2 « Difficultés des élèves »).
En d’autres termes, il est fondamental que les élèves sachent préalablement lire l’énoncé d’un problème mathématique, le comprendre, le reformuler en ses propres mots afin d’aboutir à un raisonnement logique.
Au Cameroun, la question de l’oral en mathématique, ainsi que l’analyse des interactions orales dans les salles de classe en particulier, dans les écoles primaires, a fait l’objet de peu d’études à l’heure actuelle. La présente réflexion a pour objectif d’étudier la place de la compétence langagière dans la résolution de problèmes mathématiques chez les élèves du Cours moyen 2 dans les écoles primaires. Il est question de déterminer dans quelle mesure les enseignant·es, dans leurs pratiques de classes, préparent leurs élèves à l’utilisation de la compétence langagière pour la résolution de problèmes mathématiques. Comment résoudre, de manière significative, les problèmes mathématiques dans les classes de Cours moyens 2 (CM2) où un grand nombre d’élèves ne parle pas couramment les langues d’enseignement?
Tout au long de ce travail, nous allons nous appesantir sur la situation linguistique des classes de mathématiques des CM2 des écoles primaires. En ayant recours à une approche méthodologique quantitative et qualitative, il sera question de faire un aperçu de la situation linguistique de l’école camerounaise et d’aborder les problèmes rencontrés par les élèves de ces classes, notamment celles des écoles primaires de l’arrondissement de Goulfey, dans la région de l’Extrême-Nord du Cameroun. Ensuite, nous examinerons la question de l’utilisation de la langue française au cours des leçons de mathématiques, en la mettant en rapport avec le paradigme prometteur qu’est le translanguaging. En dernier ressort, seront abordées les compétences langagières construites par les élèves impliqué·es dans la résolution de problèmes mathématiques, notamment l’habileté en lecture, la compréhension du texte informatif et la performance orale en langue d’enseignement. Des pistes de réflexion seront proposées pour mieux résoudre les problèmes mathématiques.
L’étude : le contexte, les enjeux et la méthode
La présente étude porte sur le rôle de la compétence langagière dans l’apprentissage des mathématiques dans huit écoles primaires de l’arrondissement de Goulfey, localité située dans le département du Logone-et-Chari, région de l’Extrême-Nord du Cameroun. Afin de mettre en relation l’objet de l’étude avec les circonstances sociétales, nous dresserons un tableau sommaire du paysage linguistique de l’école camerounaise. Ensuite, nous discuterons des enjeux liés à la langue d’enseignement lors de l’apprentissage dans d’autres disciplines avant d’en venir à la méthodologie adoptée pour l’étude.
Aperçu de la situation linguistique de l’école camerounaise et à Goulfey
Au Cameroun, le contexte de multilinguisme fait l’objet d’une grande attention de la part des chercheurs et chercheuses. Le Cameroun est un pays qui a subi la colonisation comme la plupart des pays africains. Cette colonisation a impacté le système éducatif à travers l’instauration du français et de l’anglais comme langues officielles. À tous les paliers éducatifs, les langues d’enseignement/apprentissage que sont le français et l’anglais ne sont pas les langues maternelles de la plupart des apprenant·es, et particulièrement pour ceux et celles des régions dites francophones. En plus, dès la classe de 4e du secondaire, l’on a introduit l’enseignement des langues vivantes II (LVII), l’objectif étant de former des citoyen·es dont le pays a besoin, c’est-à-dire capables de communiquer et d’échanger avec d’autres citoyen·es. Aussi, dans le primaire et le secondaire, les enseignant·es doivent-ils/elles non seulement enseigner les disciplines, mais aussi gérer la diversité linguistique des élèves dans leur classe.
Dans l’arrondissement de Goulfey, les langues camerounaises pratiquées sont l’arabe et le kotoko. C’est ainsi que les élèves entrent dans le système éducatif avec plusieurs langues différentes parlées et apprises dès la maison. L’arabe dit shuwa qui sert de véhiculaire au niveau du département du Logone-et-Chari est aussi parlé par des locuteurs et locutrices du kotoko (Barreteau et Dieu, 2005, paragr. 130). Le terme « kotoko » désigne pas seulement une langue, mais un groupe de plusieurs langues, selon Tourneux (2005) qui dénombre quatorze termes autonymiques par lesquels les locuteurs et locutrices désignent leur langue. Dans le cas de la région de Goulfey et ses environs, ce terme est malgbe (Tourneux, 2005). Ainsi, les élèves de Goulfey baignent donc dans un environnement multilingue notable. Il s’agit d’envisager l’apprentissage des mathématiques dans un tel environnement dans le but de dégager les habiletés nécessaires à l’accomplissement d’une tâche telle que la résolution de problèmes mathématiques.
La résolution de problèmes mathématiques chez les élèves du CM2 : une question de compétence multiple
De plus en plus, les difficultés liées à la résolution de problèmes mathématiques semblent d’ordre général et plusieurs systèmes éducatifs en souffrent. Le rapport de l’évaluation du PASEC révèle que « dans les dix pays enquêtés[1], près de 60 % des élèves, en moyenne, n’ont pas atteint le seuil “suffisant” de compétence en lecture et en mathématiques en fin de scolarité » (2016, p. 130). L’étude menée par Ourahay, El Gharras et Rouan (2015) indique qu’il existe aussi de faibles rendements scolaires en mathématiques dans les écoles primaires et les collèges du Maroc. Dans leur conclusion, Ouahay, El Gharras et Rouan posent parmi les trois principales exigences qui conditionnent l’enseignement des mathématiques, la nécessité, pour les élèves, « d’avoir un minimum de prérequis » (2015, p. 1040). La capacité à lire, à écrire et à comprendre la langue de travail fait partie de ces conditions préalables. Sur le profil de scolarisation dans l’enseignement primaire, le PASEC observe qu’entre 2004 et 2005, il y a un faible taux d’accès à la première année du primaire dans les régions septentrionales dû à deux principaux facteurs : le système d’évaluation et un déficit de la demande de scolarisation (PASEC, 2007, p. 23).
La résolution de problèmes mathématiques est une composante de la discipline. Cette composante des mathématiques est celle qui cause le plus de problèmes aux élèves de Cours moyen. Pour cela, le rendement attendu dans cette composante n’est pas la chose la mieux partagée dans les classes des Cours moyens 2 de l’arrondissement de Goulfey. Lors de la résolution de problèmes mathématiques, les élèves rencontrent d’énormes difficultés qui sont liées à la complexité et à l’interactivité des compétences qu’ils et elles doivent mettre en œuvre. L’annuaire statistique de la Délégation départementale de l’Éducation de base du Logone-et-Chari (DDEB-Kousseri) montre que les taux de réussite au Certificat d’étude primaire (CEP) de ces trois dernières années concernant les mathématiques oscillent entre 21 % et 33 % (année 2019/2020 : 27,16 %; 2020/2021 : 29,15 % et 2021/2022 : 29,96 %). Ce qui n’est donc pas un taux louable et acceptable.
Eu égard aux faibles rendements des élèves en mathématiques de Cours moyen 2 des écoles primaires de l’arrondissement de Goulfey, le ministère de l’Éducation de base (MINEDUB) a pris quelques initiatives, notamment la mise à disposition du matériel didactique dans ces écoles, tels que les livres agréés de mathématiques, l’aménagement des curriculums, l’organisation des journées pédagogiques sur des thèmes relatifs à « la résolution de problèmes mathématiques à l’école primaire », le problème d’enseignement dans les langues officielles afin de recycler les enseignant·es sur toutes les innovations pédagogiques pour réduire les faibles rendements constatés dans le domaine des mathématiques.
Au niveau de l’Inspection d’arrondissement de Goulfey, les calendriers des cellules pédagogiques sont élaborés et exécutés dans les différents bassins pédagogiques préalablement établis. Ces cellules ont pour objectif de combler les lacunes des enseignant·es. Au sein des établissements scolaires, les leçons collectives sont organisées par le chef d’établissement, puis présentées par l’animateur pédagogique dans le but d’édifier ses collègues en difficultés. Les leçons modèles sont présentées par les responsables des écoles toujours dans les disciplines où les instituteur·trices ont des difficultés, notamment en résolution de problèmes mathématiques.
Malgré ces efforts fournis par le ministère de l’Éducation de base à travers ses démembrements, le problème du faible rendement relativement à la résolution de problèmes mathématiques persiste toujours. Pourtant, la résolution de problèmes mathématiques constitue un instrument de cognition susceptible de stimuler le raisonnement, la réflexion, les inférences et l’esprit créatif chez les apprenant·es. En effet, on constate que, en matière de performance, ce sont les « élèves [qui] sont mieux équipés que d’autres pour élaborer une représentation mentale cohérente de la situation du problème, planifier les étapes pour atteindre l’objectif ciblé, adapter leur stratégie en fonction des informations qu’ils découvrent, et réfléchir aux problèmes et à leur solution » (OCDE, 2014, p. 3).
Fort de tout cela, quelques questions nécessitent d’être posées : dans quelle mesure les enseignant·es, dans leurs pratiques de classe, préparent leurs élèves à utiliser la compétence langagière pour résoudre des problèmes mathématiques? Comment résoudre de manière significative, les difficultés en mathématiques dans des classes de Cours moyen 2 où un grand nombre d’élèves ne parlent pas couramment la langue d’enseignement? Comment le translanguaging, en tant cadre réflexif novateur, peut-il mieux expliquer les approches pédagogiques dans un univers multilingue d’apprentissage de mathématiques?
Le cadre méthodologique
Dans le cadre de la présente étude, nous recourons à la méthode mixte parce qu’elle favorise l’obtention des données et résultats fiables, plus proches de la réalité. Notre population d’étude est composée d’enseignant·es et d’élèves de Cours moyen 2 des écoles primaires de l’arrondissement de Goulfey. C’est à ce niveau que le faible rendement en résolution de problèmes mathématiques mentionné lors des rencontres des Unités d’animation pédagogique (UNAPED) en 2022 est récurrent.
Pour la construction de l’échantillon de l’étude, nous avons porté notre choix sur la méthode probabiliste parce qu’elle est basée sur l’aléatoire, et elle donne la même chance à tous les individus d’être sondés. Au final, nous avons obtenu un échantillon constitué de 117 élèves des classes de CM2 des écoles choisies en fonction surtout du nombre d’élèves réellement inscrit·es, soit 56 filles et 61 garçons, puis 14 enseignant·es, réparti·es en 9 enseignants et 5 enseignantes, comme présenté dans le tableau ci-dessous.
Tableau 1. Présentation de l’échantillon
| N° | Établissements | Effectifs des élèves de CM2 | Effectifs des enseignant·es |
| 1 | École publique de Goulfey 1 (EP Goulfey 1) | 13 | 1 |
| 2 | École publique de Goulfey 2 (EP Goulfey 2) | 25 | 4 |
| 3 | École publique de Goulfey 3 (EP Goulfey 3) | 14 | 2 |
| 4 | École publique de Moulwang (EP Moulwang) | 13 | 1 |
| 5 | École publique de Mara (EP Mara) | 13 | 1 |
| 6 | École publique de Goulfey Gana (EP Goulfey Gana) | 12 | 1 |
| 7 | École publique de Hilélé (EP Hilélé) | 13 | 2 |
| 8 | École publique d’Ardébé (EP Ardébé) | 14 | 2 |
| TOTAL | 117 | 14 |
Source : enquête de terrain (2023)
Dans le cadre de cette étude, nous avons proposé un questionnaire aux élèves et confectionné un guide d’entretien pour les enseignant·es. Le questionnaire, ainsi que le guide, portent sur les variables suivantes : l’habileté en lecture, l’épreuve de compréhension de texte informatif et la performance orale en langue d’enseignement.
S’agissant du test de lecture, nous avons fait appel à un texte extrait du document intitulé Réussir au CEP et au concours d’entrée en 6e et en 1ère année, notamment l’unité 4 (Nanga Nanga et al. s.d., p. 23). Nous avons légèrement modifié le texte afin de faire intervenir la ponctuation et la prononciation des mots par les élèves. Pour le test de compréhension du texte informatif, une ancienne épreuve de compréhension de texte informatif a été proposée aux élèves de CM2. Cette épreuve a subi aussi quelques modifications afin de répondre à nos attentes par rapport au questionnaire. Un texte informatif est un texte non fictif qui, comme son nom l’indique, informe le lecteur ou la lectrice sur un sujet, à l’exemple des manuels scolaires et des manuels d’utilisation. S’agissant du test de performance orale en langue d’enseignement ou expression orale, nous avons eu recours à des images illustratives et aux questions orales pour recueillir les informations. Les images ont été extraites de divers livres afin de varier les situations de communication.
En ce qui concerne l’analyse de données issues des enquêtes de terrain, nous avons utilisé l’analyse descriptive qui a permis de dresser des tableaux sur l’ajustement du modèle et sur le coefficient de régression de R-deux de Nagelkerke. Celui-ci est pertinent dans la mesure où il permet de trouver les relations entre deux facteurs de données afin de classer les sujets en fonction des valeurs d’un ensemble de variables prédictives.
Par rapport au déroulement de l’enquête proprement dite, nous avons recueilli les informations en lecture à l’aide du test de lecture. En effet, nous soumettons l’épreuve de lecture à l’élève pour une prise de connaissance et une préparation mentale pendant environ cinq minutes avant l’activité de lecture. Puis, nous passons à la lecture proprement dite pour une durée maximale de cinq minutes. Ainsi, pendant que l’élève lit, nous remplissons le questionnaire. Quant à l’épreuve de compréhension de texte, le texte est remis à l’apprenant·e pour une durée maximale de 30 minutes.
S’agissant de la performance orale en langue d’enseignement, nous présentons les images illustratives à l’élève, puis nous lui demandons de bien observer pour décrire la scène et mesurer le niveau d’écoute et d’expression de la langue d’enseignement. Nous avons fait appel à des enseignant·es qui nous ont aidé dans le remplissage du questionnaire. Quant aux entretiens avec les enseignant·es, nous avons enregistré leurs différents propos après consentement à l’aide d’un téléphone.
Tableau 2. Opérationnalisation des variables de l’étude
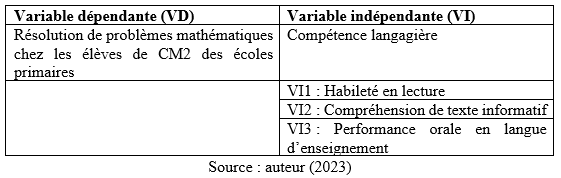
Le tableau 2 nous permet de comprendre l’opérationnalisation de nos deux variables, à savoir la variable dépendante (la résolution de problèmes mathématiques chez les élèves des CM2 des écoles primaires de l’arrondissement de Goulfey) et la variable indépendante (compétence langagière). Par ailleurs, notre variable indépendante a été opérationnalisée en trois variables, notamment l’habileté en lecture, la compréhension du texte informatif et la performance orale en langue d’enseignement.
La compétence langagière renferme une multitude d’habiletés que nous ne pourrions épuiser en une seule enquête. Nous avons alors choisi de nous intéresser à l’habileté en lecture chez les apprenant·es. Celle-ci concerne les aspects suivants : l’opération de décodage qui permet de passer des lettres aux sons, de la compréhension du vocabulaire et la capacité à réfléchir en s’appuyant sur le texte. La performance orale de la langue d’enseignement requiert l’utilisation, la capacité d’interagir dans la langue et d’interpréter des messages.
Présentation des résultats de l’enquête
Réalisée du 11 au 18 avril 2023, l’enquête recourt à deux techniques de collecte : le questionnaire et l’entretien. Dans le premier cas, il s’agit des réponses fournies par les élèves à une série de questions relatives à leur compétence langagière. Quant au second cas, il s’agit d’un entretien semi-directif réalisé avec 14 enseignant·es des classes de CM2. Les sujets abordés concernent globalement leurs pratiques de classe, notamment lors des leçons de mathématique. Nous présenterons d’abord les éléments du questionnaire avant de parler des résultats provenant de l’entretien.
Les données issues du questionnaire
Le questionnaire est organisé suivant les trois variables que sont l’habileté en lecture, la compréhension de texte informatif et la performance orale en langue d’enseignement. Les résultats obtenus sont contenus dans les tableaux ci-dessous.
Tableau 3 Information sur l’ajustement du modèle de l’habileté en lecture

Le tableau 3 sur l’ajustement du modèle de la variable « l’habileté en lecture » montre un khi-carré de 98,023 à 28 degrés de liberté, avec une significativité de 0,000 à une marge d’erreur de 10 %. Ainsi, comme 0,000 est inférieur à 0,1 alors nous pouvons valider l’existence d’un lien significatif entre l’habileté en lecture et la résolution de problèmes mathématiques par les élèves de CM2 dans les élèves primaires de l’arrondissement de Goulfey.
Tableau 4. Coefficient de régression du modèle de la variable « habileté en lecture »
| Cox et Snell | ,567 |
| Nagelkerke | ,691 |
| McFadden | ,487 |
Source : traitement des données, auteur (2023)
Le tableau 4 porte sur la vérification de la force d’association du modèle à partir d’un examen du R- deux de Nagelkerke qui représente la variance expliquée par le modèle. Dans le cadre de notre analyse, ce R-deux de Nagelkerke a une valeur de 0,691, ce qui signifie que le modèle explique 69,1 % la variance de la variable dépendante qui est la résolution de problèmes mathématiques. Nous pouvons mentionner en se référant au coefficient de Nagelkerke qui est de 0,691 qu’il existe une forte relation entre l’habileté en lecture et la résolution de problèmes mathématiques. Toutefois, il y a lieu de relever que par rapport aux informations relatives à la qualité d’ajustement du modèle à partir de la valeur du R-deux de Cox et Snell qui est de 0,567 signifiant ainsi la qualité moyenne d’ajustement du modèle.
Tableau 5. Informations sur l’ajustement du modèle de la variable « la compréhension de texte informatif »

Le tableau 5 nous donne des informations sur l’ajustement du modèle de l’influence de la compréhension de texte informatif sur la résolution de problèmes mathématiques. Il présente un khi-carré de 131,046 à 24 degrés de liberté, avec une significativité de 0,000 à une marge d’erreur de 10 %. Ainsi, comme 0,000 est inférieur à 0,1 alors nous pouvons valider l’existence d’un lien significatif entre la compréhension de texte informatif et la résolution de problèmes mathématiques par les élèves de CM2 dans les écoles primaires de l’arrondissement de Goulfey.
Tableau 6. Coefficient de régression du modèle de la variable
| Cox et Snell | ,674 |
| Nagelkerke | ,821 |
| McFadden | ,652 |
Source : auteur (2023)
Le tableau 6 nous permet de vérifier la force d’association du modèle à partir d’un examen du R- deux de Nagelkerke qui représente la variance expliquée par le modèle. Dans le cadre de notre analyse, ce R-deux de Nagelkerke a une valeur de 0,821 ce qui signifie que le modèle explique 82,1 % la variance de la variable dépendante qui est la résolution de problèmes mathématiques. L’objectif visé est de vérifier la force d’association du modèle. Nous pouvons donc conclure en se référant au coefficient de Nagelkerke qui est de 0,82 qu’il existe un lien significatif très fort entre la compréhension de texte informatif et la résolution de problèmes mathématiques. En plus, ce même tableau nous donne également des informations sur la qualité d’ajustement du modèle à partir de la valeur du R-deux de Cox et Snell qui a une valeur de 0,674, ce qui signifie que la qualité d’ajustement du modèle est moyenne.
Tableau 7. Informations sur l’ajustement du modèle sur la performance orale en langue d’enseignement

Le tableau 7 nous renseigne sur les informations sur l’ajustement du modèle sur la performance orale en langue d’enseignement. Il ressort de ce tableau, un khi-carré de 52,578 à 22 degrés de liberté, avec une significativité de 0,000 à une marge d’erreur de 10%. Ainsi, comme 0,000 est inférieur à 0,1 alors nous pouvons suggérer l’existence d’un lien significatif entre la performance orale en langue d’enseignement et la résolution de problèmes mathématiques chez les élèves de CM2 de l’arrondissement de Goulfey.
Tableau 8. Coefficient de régression du modèle
| Cox et Snell | ,362 |
| Nagelkerke | ,441 |
| McFadden | ,261 |
Source : auteur (2023)
Le tableau 8 vérifie la force d’association du modèle à partir d’un examen du R- deux de Nagelkerke qui représente la variance expliquée par le modèle. Dans le cadre de notre analyse, ce R-deux de Nagelkerke a une valeur de 0,441 ce qui signifie que le modèle explique 44,1 % la variance de la variable dépendante qui est la résolution de problèmes mathématiques. L’objectif visé étant de vérifier la force d’association du modèle, nous pouvons donc conclure en se référant au coefficient de Nagelkerke qui est de 0,441 qu’il existe un lien significatif faible entre la performance orale en langue d’enseignement et la résolution de problèmes mathématiques. En outre, par rapport à la qualité d’ajustement du modèle à partir de la valeur du R-deux de Cox et Snell qui a une valeur de 0,362 signifiant que le modèle a une qualité faiblement ajustée.
Les données issues du guide d’entretien
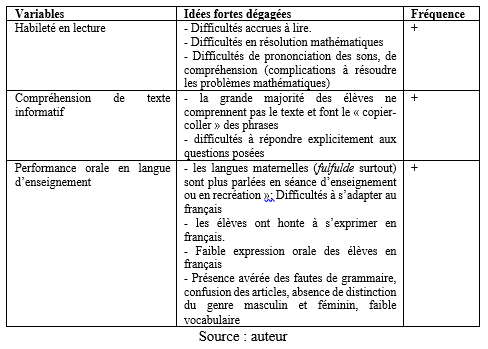
L’entretien avec les enseignant·es abordent les questions concernent l’habileté en lecture, la compréhension et la performance des apprenant·es dans la langue d’enseignement. Les résultats ont été enregistrés dans le tableau suivant[2].
Tableau 9. Analyse synthétique du contenu des avis des enseignant·es
Quelles implications pour l’apprentissage des mathématiques?
Au regard de ces résultats, il importe de tirer un certain nombre d’implications en rapport avec l’habileté en lecture, la compréhension du texte informatif et la performance orale en langue d’enseignement. Nous clôturerons en présentant, en guise de perspectives, le translanguaging, nouvelle approche plus adéquate pour les classes en situation de multilinguisme.
L’habileté en lecture et la résolution de problèmes mathématiques
D’après les résultats de l’analyse des données recueillies, il existe un lien significatif entre l’habileté en lecture et la résolution de problèmes mathématiques. Ceci s’explique par l’obtention d’un khi-carré d’une valeur de 98,023 à 28 degrés de liberté, avec une significativité de 0,000 inférieur à 0,1. Aussi le coefficient de Nagelkerke d’une valeur de 0,691 a-t-il permis de montrer la force d’association du modèle, puis le coefficient de Cox et Snell d’une valeur de 0,567 a permis de dire que la qualité d’ajustement du modèle est moyenne. Par ailleurs, l’analyse de contenus issus des entretiens avec les enseignant·es des différentes écoles primaires de l’arrondissement de Goulfey a permis d’expliquer qu’il y a une relation significative entre l’habileté en lecture et la résolution de problèmes mathématiques.
En effet, il y a lieu de relever que la résolution d’un problème mathématique serait tributaire du savoir lire de l’enfant lors de l’apprentissage. C’est dans cette perspective que nos résultats corroborent ceux obtenus par Forest et Voyer (2011) lorsqu’ils affirment que la lecture permet de construire le sens d’un problème écrit afin de parvenir à sa résolution. En outre, selon Eysseric (2004), les mathématiques sont une discipline qui recourt non seulement à la langue usuelle dans le cadre de son apprentissage, mais aussi un autre langage qu’on met en place en définissant des éléments codiques spécifiques. Au niveau des écoles primaires de l’arrondissement de Goulfey, les activités mathématiques développées par les enseignant·es font appel prioritairement à la langue française ou anglaise tant dans la transmission des savoirs que dans la présentation des travaux à effectuer ou dans les productions des élèves.
De plus en plus, il y a des élèves qui utilisent leur langue maternelle quand ils et elles font les activités en mathématiques. Nos résultats trouvent leur fondement dans les travaux de Eysseric (2004) en ce sens que l’habileté en lecture influe sur la résolution de problèmes mathématiques. En effet, il faut veiller à ce que les difficultés de lecture ne viennent pas gêner les progrès en mathématiques dont sont capables les élèves. D’où l’importance d’une dimension orale dans le travail en mathématiques pour que l’élève parvienne à comprendre la situation évoquée et la question posée, et à commencer alors à résoudre les problèmes mathématiques. Les opinions des enseignant·es interrogé·es confirment le fait que l’habileté en lecture conditionne la résolution de problèmes mathématiques quand E1 déclare :
Chez moi, les élèves ne lisent pas bien, ils ont aussi des problèmes à bien prononcer les sons, la majorité ne lit pas. Ces enfants ne comprennent pas les problèmes, ils ne connaissent pas ce qu’on leur demande de faire puisqu’ils ne connaissent pas lire. Ce qui fait que pour résoudre un problème ça devient compliqué (E1 de l’EP Ardebé).
L’habileté en lecture chez les élèves constitue un élément non négligeable dans le cadre de la résolution de problèmes mathématiques. En effet, la spécificité des textes utilisés en mathématiques demande un travail particulier relatif à leur lecture (Radford et Barwell, 2016)). En outre, les textes utilisés en mathématiques ne sont pas les mêmes que ceux rencontrés en littérature ou dans d’autres disciplines et leurs particularités doivent être prises en compte dans les apprentissages (Eysseric, 2004). Spécifiquement, selon un enseignant (E2) de l’EP Goulfey 1,
Parvenir à lire facilement un texte en français influence la résolution de problèmes en mathématiques. Dans ma classe, ceux qui savent lire et comprennent le sens des questions posées réussissent facilement à résoudre les problèmes en mathématiques. De mon point de vue, nos élèves n’ont pas de compétences langagières assez avérées pour comprendre même le français qui écrit. Parfois, nous-mêmes enseignants ne parvenons pas à cerner le français qui est écrit. Nos élèves ont raison de ne pas comprendre ce qui est écrit surtout par des chercheurs chevronnés (propos d’un enseignant de l’EP Groupe 1 de Goulfey, recueillis le 11 mai 2023 par téléphone).
C’est pour cette raison que dans les cours à l’école primaire, la plupart des enseignant·es se retrouvent parfois dans l’obligation d’organiser des cours de soutien en français dans leurs classes. Ce qui fait qu’ils et elles apprennent aux élèves à lire des énoncés de mathématiques sans jamais résoudre les problèmes en question. On sait que ce type de pratique n’a visiblement aucun effet sur les compétences des enfants dans la résolution de problèmes (Matheron, 2002). Dans la pratique des enseignant·es des écoles primaires de l’arrondissement de Goulfey, on note que les enseignements dans d’autres disciplines sont menés conjointement avec la pratique des activités mathématiques. En effet, l’habileté en lecture influence la résolution de problèmes mathématiques dans la mesure où l’apprentissage de la lecture de textes mathématiques pourra être encouragé par la présence en classe de supports variés contenant des écrits mathématiques mis à la disposition des enfants (Mercier, 1995).
Pour résoudre un problème mathématique, il est recommandé de savoir lire (Assude, Sackur et Maurel, 1999). La lecture apparaît ainsi comme un processus interactif de résolution de problème qui vise à construire le sens d’un texte. C’est ainsi qu’un enseignant (E4) affirme :
L’habileté en lecture chez nos élèves est une question très importante, car les cours de mathématiques nécessitent de maîtriser la langue d’enseignement/apprentissage qu’est le français. Son influence est significative dans la résolution de problèmes mathématiques que nous leur proposons (avis d’un enseignant, EP de Goulfey 2, recueilli le 11 mai 2023).
Nos résultats vont dans le sens des aspects mis en exergue par Forest et Voyer (2021); Goulet et Voyer (2014) qui pensent que les apprenant·es doivent reformuler le texte lu en exposant les informations cachées du texte. C’est dans ce sens que le modèle du translanguaging est intéressant dans cette recherche, car il permet à l’enseignant·e de développer chez l’élève une grande capacité de langues, permettant à ce dernier de lire, de comprendre et même d’inférer pour un rendement meilleur en ce qui concerne la résolution de problèmes mathématiques. Nos résultats vont dans le même sens que ceux de Séka Yapi (2021) qui fait état des découvertes importantes sur les langues africaines en expliquant la suprématie des locuteurs natifs (de la langue maternelle) en termes de performance, dans la résolution des problèmes en mathématique et des raisonnements logiques.
L’habileté en lecture a un effet positif sur les performances des élèves des Cours moyens en résolution de problèmes mathématiques dans l’arrondissement de Goulfey. Les résultats de cette analyse quantitative se confirment à travers les propos de l’enseignante E12 qui précise que « la lecture va de pair avec les mathématiques. Un élève qui éprouve des difficultés à lire ne pourra pas comprendre la question posée afin d’apporter les éléments de réponses. Dans ma classe, sur 62 élèves, j’ai 15 élèves qui se sentent à l’aise en résolution de problèmes mathématiques parce qu’ils lisent bien » (propos d’une enseignante de l’EP Groupe 2 de Goulfey, recueillis le 12 mai 2023).
On note, en effet, qu’il n’est pas question d’aborder la résolution de problèmes mathématiques sans toutefois avoir des aptitudes ou des capacités en lecture. Cette habileté en lecture contribue grandement à la construction du sens d’un texte (Sensevy, 2011; Assude, Sackur et Maurel, 1999b).
La compréhension du texte informatif
D’après les résultats de l’analyse des données recueillies, il existe un lien significatif entre la compréhension du texte informatif et la résolution de problèmes mathématiques. Ceci se justifie par l’obtention d’un khi-carré d’une valeur de 131,046 à 24 degrés de liberté, avec une significativité de 0,000 inférieur à 0,1. Aussi le coefficient de Nagelkerke d’une valeur de 0,821 a-t-il montré la force d’association du modèle, puis le coefficient de Cox et Snell d’une valeur de 0,674 a permis de dire que la qualité d’ajustement du modèle est moyenne.
Dans le cadre de cette étude, la compréhension du texte informatif par les élèves des Cours moyens 2 de l’arrondissement de Goulfey influence positivement la résolution de problèmes mathématiques. Ceci se justifie par les résultats d’analyse qui indiquent que les questions explicites, implicites ou inférentielles et les informations utiles sont des indicateurs privilégiés de la compréhension de texte informatif et ayant un effet spécifique sur la résolution de problèmes mathématiques.
En effet, nos résultats de recherche rejoignent ceux issus des travaux de Forest et Voyer (2021) qui ont étudié les effets du type de texte sur les performances scolaires des élèves notamment en ce qui concerne la résolution de problèmes mathématiques. Selon l’enseignante E3, « le peu d’élèves qui lisent bien s’en sortent en compréhension de texte informatif. Mais par contre, pour ceux qui ne savent pas lire, ils recopient seulement le texte et le collent à l’endroit prévu pour la réponse » (propos d’une enseignante de l’EP de Goulfey-Gana, recueillis le 12 mai 2023 à Goulfey). Nous notons ici que la compréhension de texte informatif ne passe pas très bien, surtout pour ceux et celles des apprenant·es ayant des lacunes en lecture. Ce manquement pourrait expliquer le faible rendement des élèves en résolution de problèmes mathématiques. C’est pour cette raison que l’enseignant E6 affirme : « Mes élèves ne s’en sortent pas facilement en ce qui concerne les questions inférentielles, on a des sérieux problèmes à ce niveau, les élèves laissent le vide. Il faut toujours revenir avec quelques exemples pour les amener à sortir vraiment la réponse juste, sinon ils se perdent » (propos d’un enseignant de l’EP de Moulouang, recueillis le 12 mai 2023 par téléphone). Une autre enseignante renchérit en déclarant :
Il y en a qui répondent exactement aux questions du fait qu’ils ont compris le texte. Par contre, il y en a ceux qui lisent et ne comprennent pas, et ne parviennent pas à répondre aux questions explicites. N’en parlons pas alors pour les questions implicites. Il y a donc un problème récurrent de compréhension de textes chez nos élèves, car il faut d’abord comprendre le texte pour pouvoir répondre aux questions posées (propos d’une enseignante de l’EP Groupe 1 de Goulfey recueillis le 11 mai 2023 à Goulfey).
L’analyse des contenus issue des entretiens avec les enseignant·es des écoles primaires de l’arrondissement de Goulfey indique que les élèves ont des difficultés à répondre aux questions du fait de leur incapacité à raisonner. Or, en résolution de problèmes mathématiques, les inférences sont presque indispensables, ce qui peut expliquer le faible rendement que nous rencontrons chez la grande majorité des élèves des écoles de l’arrondissement de Goulfey. Pour l’enseignant E10, « ceux des élèves qui s’en sortent réellement en compréhension du texte informatif sont ceux qui comprennent le message caché dans le texte. Présentement, le pourcentage est encore très faible, 20 % au trop travaillent bien dans ma classe » (propos d’un enseignant de l’EP groupe 3 de Goulfey recueillis le 12 mai 2023 à Goulfey). Ce qui confirme les difficultés des apprenant·es en compréhension du texte informatif.
Pourtant, d’après les travaux de Kintsch et Greeno (1985), résoudre un problème mathématique passe par trois phases : la première phase est la construction de la base de texte qui consiste pour l’élève à lire le texte de l’énoncé afin de faire ressortir les informations utiles. La deuxième phase est la construction d’une représentation mathématique permettant aux élèves d’établir le lien entre la question posée et la démarche de résolution. À ce niveau, l’élève interprète chaque énoncé de la base de texte en fonction de la résolution du problème puis se construit une représentation mathématique. Enfin, la troisième phase est la construction d’un plan de solution qui consiste pour l’élève à prévoir les étapes nécessaires pour trouver la solution au problème. L’élève doit donc bonifier l’information fournie par le texte en s’appuyant sur ses propres connaissances et sur ses expériences pour arriver à une interprétation personnelle du texte. Ceci se justifie par l’usage du modèle de translanguaging mis en exergue dans le cadre de cette étude.
La performance orale en langue d’enseignement
D’après les résultats de l’analyse des données recueillies, il existe un lien significatif entre la maîtrise de la langue orale d’enseignement et la résolution de problèmes mathématiques. Ceci s’explique par l’obtention d’un khi-carré d’une valeur de 52,578 à 22 degrés de liberté, avec une significativité de 0,000 inférieur à 0,1. Aussi le coefficient de Nagelkerke d’une valeur de 0,441 montre-t-il la force d’association du modèle, puis le coefficient de Cox et Snell d’une valeur de 0,362 a permis de dire que le modèle a une qualité faiblement ajustée.
Au regard des propos des enseignants et enseignantes, la performance orale en langue d’enseignement au Cameroun (français et anglais) a un impact positif sur le rendement des élèves des Cours moyens 2 en résolution de problèmes mathématiques des écoles primaires de l’arrondissement de Goulfey. Cet état de fait est confirmé par les propos d’une enseignante E11 : « En général, les élèves s’expriment en kotoko ou en arabe choa, c’est la langue la plus parlée à l’école, que ce soit en séance d’enseignement ou pendant la recréation » (propos d’une enseignante de l’EP de Mara, recueillis le 13 mai 2023 à Goulfey). C’est en cela que le modèle du translanguaguing se justifie dans cette recherche. Il y a lieu de souligner que nos résultats corroborent les nombreuses études menées dans le contexte de l’enseignement des mathématiques en contexte multilingue (Culligan et Wagner, 2015; Cenoz, 2017). Ces recherches valorisent les ressources linguistiques que les élèves peuvent apporter à l’apprentissage des mathématiques. Elles mettent en avant les apports du nouveau paradigme qu’est le translanguaging qui donne du sens à la compréhension et à l’acquisition des connaissances à travers l’utilisation de deux ou plusieurs langues (Baker, 2011). Les propos d’un enseignant E6 renforce cette position en déclarant que
Nous sommes dans une région où les langues véhiculaires sont le kotoko et l’arabe choa. Aujourd’hui plus de 99 % des élèves sont habitués à ces langues. Pour qu’ils s’adaptent surtout au français c’est difficile. En plus, ils ont souvent les problèmes de prononciation et d’articulation des mots. Parfois, ils ont même honte de s’exprimer en public. Pour d’autres élèves, c’est le manque de volonté. Donc l’expression orale dans ma classe est faible, les élèves qui s’expriment oralement et couramment en français sont minoritaires (propos d’un enseignant de l’EP de Moulwang recueillis le 11 mai 2023 par téléphone).
Nous constatons avec les enseignants et enseignantes que la performance orale en langue d’enseignement n’est pas la chose la mieux partagée chez la grande majorité des élèves des écoles primaires de l’arrondissement de Goulfey. Nous savons pertinemment que la langue orale d’enseignement est un vecteur de la transmission du savoir. C’est grâce à elle que les échanges et interactions dans la salle de classe sont possibles. Ainsi, une non-maîtrise de la langue pourrait conduire à une incompréhension des enseignements et, par conséquent, à un mauvais rendement scolaire en général, et en résolution de problèmes mathématiques en particulier. Toutefois, l’enseignant E1 déclare : « Quand bien même les élèves s’expriment, il y a toujours les fautes de grammaire qui interviennent, ils confondent les articles, ils ne distinguent pas le masculin du féminin, ils ont un vocabulaire faible et confondent tout » (propos d’un enseignant de l’EP Hilélé recueillis le 12 mai 2023 par téléphone). Une autre enseignante de renchérir : « Je pense que nos élèves ne s’expriment pas correctement en français surtout. Normalement, au CM1 et CM2, ils sont censés parler couramment et bien, mais ils ne parviennent pas, ils ne s’en sortent pas. Ils éprouvent énormément des difficultés » (propos d’une enseignante de l’EP Ardébé recueillis le 11 mai 2023 par téléphone). Ces propos vont dans le même sens que Bessonnat (1998) qui affirme que la source des difficultés des élèves en mathématiques au primaire serait largement imputable à des problèmes d’expression et de compréhension de la langue.
Ainsi, l’apprenant·e acquiert son savoir à travers les échanges entre l’enseignant·e et lui-même ou elle-même et également entre pairs (élève-élève). C’est l’idée de Lauret (1996) lorsqu’elle dit que la maitrise de la langue est l’un des principaux moyens pour comprendre et se faire comprendre. En général, les situations problèmes ont besoin d’être reformulées pour leurs meilleures compréhensions. Bien plus, les mathématiques recourent à l’usage complexe de la langue courante et mobilisent des pratiques langagières qui leur sont spécifiques. C’est pourquoi le travail de la langue et de ses usages en cours de mathématique est indispensable (Bessonnat, 1998).
Dans un contexte éducatif comme celui du département du Logone-et-Chari, la langue française est utilisée dans des situations variées et à des fins différentes. De plus en plus, cette langue n’est plus seulement considérée comme un but en soi, mais plutôt comme un outil par lequel les élèves interagissent avec leurs ami·es et leurs camarades à l’école. C’est un canal par lequel ils et elles apprennent des contenus d’enseignement dans des matières comme les mathématiques, les sciences, l’histoire, etc. En effet, les élèves doivent être capables de s’exprimer dans la langue d’enseignement et de la comprendre afin de fournir un meilleur rendement, notamment pour le cas spécifique de la résolution de problèmes mathématiques. Ce qui n’est pas le cas des élèves des écoles primaires de l’arrondissement de Goulfey. La performance orale en langue d’enseignement joue un rôle primordial dans le processus enseignement/apprentissage des mathématiques (Radford et Barwell, 2016).
Certes, les mathématiques ont une langue (symboles, formule, statistiques, etc.), mais le langage verbal est toujours nécessaire pour les commentaires, la discussion et l’enseignement. Le modèle du translanguaging milite également en faveur de la maîtrise d’autres langues qui doivent être prises en compte par les enseignants et enseignantes, car cette théorie reconnaît que l’élève est actif·ve dans la construction de ses propres connaissances à travers des interactions sociales telles que les travaux en groupe, les dialogues, les discussions, les jeux de questions-réponses et bien d’autres. Cette théorie favorise la médiation sociale dans l’apprentissage, ce qui pourrait bel et bien conduire à un rendement scolaire en général, et en résolution de problèmes mathématiques en particulier.
Le « translanguaging » : quel paradigme pour les approches pédagogiques dans les classes de mathématiques multilingues?
Il y a lieu de noter que la maîtrise de la langue est une donnée très déterminante pour la réflexion mentale, mais également pour les apprentissages mathématiques (Vlassis, 2018). Depuis la diffusion des travaux de Vygotsky et leur prise en considération en mathématiques, la communication et les interactions sociales sont considérées comme variables indissociables de l’apprentissage et de la pensée (Vlassis, Mancuso et Poncelet, 2014). Cette situation fait de la langue un outil médiateur par excellence dans le translanguaging.
De plus en plus, de nombreuses études menées dans le cadre de l’enseignement des mathématiques en contexte multilingue (Culligan et Wagner, 2015; Cenoz, 2017; Vlassis, Mancuso Giovanna, Poncelet, 2014) s’intéressent à la perspective consistant à valoriser les ressources que les apprenants et apprenantes apportent en classe de mathématiques plutôt que de cibler leurs manques. En effet, le translanguaging vise à donner du sens ainsi qu’à façonner l’expérience, la compréhension et les connaissances à travers l’utilisation de deux ou plusieurs langues (Baker, cité par Vlassis (2018).
Ce concept qui a été largement utilisé par Vlassis (2014; 2015; 2018) comme une stratégie d’enseignement efficace dans les classes multilingues est désormais utilisé pour référer aux différentes pratiques logiques dans les contextes bilingues et multilingues partout dans le monde (Cenoz, 2017). Le translanguaging s’ancre dans les pratiques langagières utilisées dans les communications multilingues. Les frontières entre les langues deviennent plus souples et les ressources spécifiques des locuteurs sont perçues comme un important support pédagogique. Le translanguaging implique de multiples pratiques discursives dans lesquelles les apprenants et apprenantes s’engagent dans leurs environnements multilingues (García, 2009).
Dans le cadre de notre étude, l’intérêt majeur de ce type de paradigme basé sur le translanguaging répond à la fois à la problématique des apprentissages des langues en mettant en exergue l’importance de la notion d’activités et de diversité des pratiques qui donne sens aux apprentissages langagiers, mais également aux principes de l’enseignement des mathématiques (Vlassis, 2018). En clair, au-delà du français ou de l’anglais auquel recourent les élèves en classe de mathématiques, le translanguaging voudrait que ces élèves se servent aussi de leurs langues maternelles ou autres langues qu’ils maîtrisent plus pour apprendre les mathématiques.
Conclusion
Dans le cadre de cette étude, nous avons examiné la place de la compétence langagière dans la résolution de problèmes mathématiques chez les élèves des Cours moyens 2 des écoles primaires de l’arrondissement de Goulfey en s’appuyant sur des variables comme le contexte de l’habileté en lecture, la compréhension du texte informatif et la performance orale en langue d’enseignement. Les analyses montrent que ces variables ont une influence positive sur la résolution de problèmes mathématiques chez les élèves des cours des CM2 de l’arrondissement de Goulfey.
En effet, la résolution de problème est une activité importante dans l’apprentissage des mathématiques, mais aussi dans l’apprentissage de plusieurs autres matières scolaires. Cette activité laisse par contre très peu d’emprise aux enseignants et enseignantes qui veulent aider leurs élèves à mieux comprendre les situations problèmes proposées dans les manuels scolaires. Il s’agit là bien plus qu’une question d’ouverture aux autres langues natives. Cela renvoie à la conception même des mathématiques qui ne peuvent être considérées comme une matière indépendante du langage, mais aussi à celle des pratiques de classe où l’apprentissage des élèves est vu comme leur participation au discours mathématique en utilisant diverses langues ainsi que différents modes d’expression.
L’habileté en lecture est une compétence à développer, car elle permet de renforcer la mémoire et les capacités cognitives de l’apprenant ou de l’apprenante. Selon Vlassis, « la compréhension de texte qui est l’aptitude à construire du sens » (2018, p. 4) est tout aussi importante. Elle est orientée dans notre étude vers le texte informatif et la capacité des élèves à faire des inférences pouvant s’expliquer dans le cadre de notre réflexion par le modèle du translanguaging (Vlassis, 2018). La performance orale en langue d’enseignement, quant à elle, occupe une place prépondérante dans le processus enseignement/apprentissage (Vlassis, Fagnant et Demonty, 2015). C’est grâce à elle que les échanges et les interactions dans la salle de classe sont possibles.
Au regard de la problématique langagière récurrente, il semble indispensable d’encourager les enseignants et enseignantes intervenant en mathématiques à repenser leurs pratiques pédagogiques en insistant sur la dimension langagière où l’oral joue le rôle de médiateur entre le langage vernaculaire de l’élève et le langage de la discipline. Des séances de travail spécifiques pourront être menées avec les élèves sur l’acquisition de compétences langagières afin de donner du sens à l’utilisation spécifique et nécessaire de la langue de la matière enseignée.
Nous espérons que cette réflexion pourra contribuer à mieux cerner et caractériser les interactions langagières dans la résolution de problèmes mathématiques dans des classes multilingues. Il serait intéressant pour les enseignants et enseignantes d’intégrer de façon consciente l’oral dans l’enseignement des mathématiques. Ils ou elles doivent développer chez les élèves l’appétence et les compétences nécessaires pour les amener à s’exprimer avec aisance à l’écrit surtout pour résoudre les problèmes mathématiques. Or, plusieurs enseignants et enseignantes intervenant dans les CM2 des écoles primaires de l’arrondissement de Goulfey qui semblent désavouer la compétence langagière en classe.
Références
Assude, Teresa, Sackur, Catherine et Maurel, Maryse. 1999. CESAME: The Personal History of Learning Mathematics in the Classroom. An Analysis of Students’ Narratives. The Philosophy of Mathematics Education Journal, 11, 88-94.
Baker, Collin. 2011. Foundations of Bilingual. Education and Bilingualism (5th edition.). Clevedon : Multilingual Matters.
Barreteau, Daniel et Dieu, Michel. 2005. Linguistique. Dans Seignobos, Christian et Iyébi-Mandjek, Olivier (dir.), Atlas de la province Extrême-Nord Cameroun. IRD Éditions. https://doi.org/10.4000/books.irdeditions.11562.
Beacco, Jean-Claude & Vollmer, Helmut Johannes. 2010. Langues et matières scolaires. Dimensions linguistiques de la construction des connaissances dans les curriculums. Strasbourg : conseil de l’Europe, Division des politiques linguistiques.
Bessonnat, Daniel. 1998. Maîtrise de la langue et apprentissages disciplinaires. Revue internationale d’éducation de Sèvres, 19, 41-48. https://doi.org/10.4000/ries.2860
Cenoz, Jasone. 2017. Translanguaging in School Contexts: International Perspectives. Journal of Language, Identity and Education 16 (4), 193–98. https://doi.org/10.1080/15348458.2017.1327816
Culligan, Karla et Wagner, David. 2015. Mathematics, Language, and Degrees of Certainty: Bilingual Students’ Mathematical Communication and Probability. Dans Bartell, Tonya Gau, Bieda N. Kristen, Putman, T. Ralph, Bradfield, Kenneth, Dominguez, Higinio (éd.), Critical Responses to Enduring Challenges in Mathematics Education. Proceedings Thirty Seventh Annual Meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education (1022-1029), East Lansing, 5-8 novembre.
Eysseric, Pirre. 2004. Albums et mathématiques. Actes du congrès de l’Association générale des enseignants des écoles et classes maternelles publiques (AGEEM). Martigues.
Forest, Marie-Pier et Voyer, David. 2021. Comment profiter de l’habileté en lecture des élèves pour réduire leurs difficultés en résolution de problèmes écrits mathématiques? TA@l’école. https://www.taalecole.ca/difficultes-ecrits-mathematiques/
Forest, Marie-Pier et Voyer, Dominic (dir.). 2022. Les principes de flexibilité de la pédagogie universelle : une voie à privilégier pour soutenir les étudiants universitaires en contexte de formation en ligne. Dans Nafti-Malherbe, Catherine, Laroui, Rakia et Égido Portela, Angel, Savoirs et environnements numériques. Innovations, mutations et consolidations dans les échanges universitaires (37-46). Montréal, Québec. Éditions JFD.
García, Ofelia. 2009. Bilingual Education in the 21st Century: A Global Perspective. Oxford: Wiley-Blackwell.
Giasson, Joceline. 2011. La lecture : difficultés et apprentissage. Boucherville : Gaétan Morin.
Kinsch, Walter et Greeno, James. 1985. Understanding and solving word arithmetic problems. Psychology review, 92 (1), 109-129. https://doi.org/10.1037/0033-295X.92.1.109
Kintsch, Walter et Greeno, James Gordon. 1985. Understanding and Solving Word Arithmetic Problems. Psychological Review, 92 (1), 109-129. https://doi.org/10.1037/0033-295X.92.1.109
Lauret, Jean-Marc. 1996. Maîtrise de la langue française et compréhension en mathématiques. Thèse de Doctorat en linguistique. Université de Paris 7.
Matheron, Yves. 2001. Une modélisation pour l’étude didactique de la mémoire. Recherches en didactique des mathématiques, 21 (3), 207–246. https://revue-rdm.com/2001/une-modelisation-pour-l-etude/
Mercier, Alain. 1995. La biographie didactique d’un élève et les contraintes temporelles de l’enseignement. Un cas en calcul algébrique. Recherches en didactique des mathématiques, 15 (1), 97-142. https://revue-rdm.com/2005/la-biographie-didactique-d-un/
Ministère de l’éducation de base. 2018. Curriculum de l’enseignement primaire francophone camerounais. Niveau 3 : cycle des approfondissements (CM1-CM2).
Mullis, Ina, Martin, Michael, Foy, Pierre and Arora, Alka. 2012. Trends in Mathematics and Science Study – TIMSS 2011: International Results in Mathematics. Amsterdam: International Association for the Evaluation of Educational Achievements (IEA).
Ness, Molly. 2011. Teachers’ Use of and Attitudes Toward Informational Text in K–5 Classrooms. Reading Psychology, 32 (1), 28-53. https://doi.org/10.1080/02702710903241322
Organisation de coopération et de développement économiques – OCDE. 2014. Trouver des solutions créatives : Quelles sont les compétences des jeunes de 15 ans en résolution de problèmes. PISA à la loupe, 38. https://doi.org/10.1787/5jz6zgzmkbhj-fr
Ourahay, Mustapha, El Gharras, Somaya, Rouan, Omar. 2015. Essai d’explication du niveau faible des performances mathématiques des élèves marocains des cycles primaire et secondaire collégial. Dans Theis, Laurent (dir.), Pluralités culturelles et universalité des mathématiques : enjeux et perspectives pour leur enseignement et leur apprentissage. Actes du Colloque Espace mathématique francophone – EMF 2015 (1028-1041). Alger, 10-14 octobre.
Programme d’analyse des systèmes éducatifs de la CONFEMEN – PASEC. 2007. Rapport Cameron 2004-2005 : le défi de la scolarisation universelle de qualité. CONFEMEN/Ministère de l’éducation de base.
Programme d’analyse des systèmes éducatifs de la Conférence des ministres de l’Éducation des États et Gouvernements de la francophonie (CONFEMEN) – PASEC. 2016. PASEC 2014 – Performance du système éducatif camerounais : compétence et facteurs de réussite au primaire. Dakar : CONFEMEN.
Radford, Luis et Barwell, Richard. 2016. Language in Mathematics Education Research. Gutiérrez, Ángel, Leder, Gilah C. et Boero, Paulo (dir.), The Second Handbook of Research on the Psychology of Mathematics Education, (275–313). Rotterdam : Brill.
Reusser, Kurt. 1990. From Text to Situation to Equation: Cognitive Simulation of Understanding and Solving Mathematical Word Problems. Dans Mandl, Heinz, De Corte, Erik, Bennett, Neville, Friedrich, Helmut Felix. Analysis of complex skills and complex knowledge domains. Oxford: Pergamon Press (477-498).
Romain, Martin, Houssemend, Claude et Brunner, Martin. 2008. Quelles conclusions peut-on tirer de l’étude PISA en ce qui concerne le fonctionnement de l’école luxembourgeoise? Dans Martin, Romain, Dierendonck, Christophe, Meyers, Christian et Noesen, Melanie (dir.), La place de l’école dans la société luxembourgeoise de demain : vers de nouveaux modèles de fonctionnement du système éducatif (187-209). De Boeck Supérieur.
Séka Yapi, Arsène Thierry. 2021. Place des langues africaines dans l’enseignement des mathématiques à l’école primaire : une analyse transversale du cas ivoirien. Cross-cultural Communication, 74 (4), 81-88. http://dx.doi.org/10.3968/12362
Sensevy, Gérard. 2011. Le sens du savoir. Éléments pour une théorie de l’action conjointe en didactique. Bruxelles : De Boeck.
Tadadjeu, Maurice. 2015. Écoles rurales électroniques en langues africaines. Expérimentation au Cameroun et orientation politique panafricaine. L’Harmattan.
Tourneux, Henry. 2005. La numération dans les parlers « kotoko » du Cameroun. Dans Mengozzi, Alberto (dir.), Studi afroasiatici : XI Incontro italiano di linguistica camitosemitica (113-124). Milano : Francoangeli.
Vlassis, Joëlle, Fagnant, Annick et Demonty, Isabelle. 2015. Symboliser et conceptualiser, deux facettes indissociables de la pensée mathématique : l’exemple de l’algèbre. Dans Thies, Laurent (dir.), Pluralités culturelles et universalité des mathématiques : enjeux et perspectives pour leur enseignement et leur apprentissage. Actes du colloque Espace mathématique francophone – EMF, (357-369), Alger, 10-14 octobre.
Vlassis, Joëlle, Mancuso, Giovanna et Poncelet, Débora. 2014. Le rôle des problèmes dans l’enseignement des mathématiques : analyse des croyances d’enseignants du primaire. Cahiers des sciences de l’éducation, 36, 143-174.
Vlassis, Joëlle. 2018. Mathématiques et langage : le cas des classes multilingues, un défi pour l’enseignement luxembourgeois. Dans Abboud, Maha (éd.), Mathématiques en scène, des ponts entre les disciplines. Actes du colloque d’Espace mathématique francophone – EMF (919-926), Paris-Gennevilliers, 22-26 octobre.
